Shapoklyak-85@narod.ru

Учеба:

Alma Mater

Институты Москвы (государственные)

Предметы:

Экономическая теория
-Вопросы к зачету ЭТ
-Электронный учебник
-Образовательный портал
-Галерея экономистов

Мировая экономика
-Вопросы к зачету МЭ
-Вариации на тему "Ответы на вопросы МЭ"

История экономических учений
-Вопросы к зачету ИЭУ

Правоведение
-Лекция №1
-Лекция №2,3
-Лекция №4
-Лекция №5
-Лекция №6
-Лекция №7
-Лекция №8
-Вопросы к зачету/экзамену
-Ответы

Философия
-Вопросы к экзамену

Информатика
-Вопросы к экзамену

Статистика
-Лекция №1
-Лекция №2
-Лекция №3
-Лекция №4
-Лекция №5
-Лекция №6
-Лекция №7
-Лекция №8
-Лекция №9
-Вопросы к экзамену

Курсовая работа по статистике, 1999 г.

shapoklyak-85

Shapoklyak-85 » Лекция №2

Абсолютные величины в статистике.
Выражают размеры явлений.
Всегда имеют размерность.
Применяются натуральные, стоимостные и трудовые величины.
Натуральные абсолютные величины соответствуют природным или потребительским свойствам предмета и выражаются в весе, штуках и т.д.
Применяются условно-натуральные абсолютные величины при суммировании однокачественной, но разнокалиберной продукции.
Натуральные единицы могут быть составными (сложными), отражающими сочетание двух результативных сторон явления (грузооборот транспорта – в тонно-километрах).
Стоимостные единицы измеряются в рублях и другой валюте.
+ - самая универсальная
- - в условиях инфляции стоимостных показателей при их сравнении во времени надо доводить до уровня совпадения.
Трудовые единицы относятся к работнику и его труду.
Простые трудовые единицы измерения – часы, человек, дни, бригады.
Составные – человек/дни, человек/час, бригада/час.
Применяются для определения объема работ.
Виды абсолютных величин: 1. Индивидуальные
2. Сводные (суммарные) – сводка, группировка индивидуальной величины.

Относительные величины.
Относительные показатели получают путем сравнения двух величин: сравниваемого периода к базе сравнения.
Относительный показатель, полученный путем сравнения двух одинаковых относительных показателей – единичный.
Пример: рентабельность – относительный показатель.
Все виды относительных величин не имеют размерностей.
Исключение – интенсивность.
Основные формы:
1. Коэффициенты (доли)
2. Проценты
Имеют форму коэффициента, если относительные показатели исчисляются простым делением (база сравнения равна 1).
Если коэффициент умножить на 100, то получим результат сопоставления в процентах (база сравнения равна 100).
Если коэффициент умножить на 1000, то получим результат сопоставления в промилле (база сравнения равна 1000).
Если коэффициент умножить на 10000, то получим результат сопоставления в продецимилле (база сравнения равна 10000).
Такое увеличение делается с целью уменьшения ошибки вычисления.

Виды относительных величин
1. процент выполнения договорных обязательств (планов)
2. относительная величина динамики (изучения явления во времени)
3. относительная величина сравнения
В результате сравнения однотипных признаков у однокачественных явлений.
4. относительная величина структуры – отношение части к целому
Характеризует долю (удельный вес в процентах) отдельных частей в общем объеме статистической совокупности
5. относительные показатели координации – отношения одной части статистической совокупности к другой
6. относительные показатели интенсивности (имеют размерность).
Пример: затраты на рубль продукции.

Средняя величина в статистике.
Средняя величина, обобщающая характеристики варьирующего признака единиц совокупности.
Условия применения:
- Массовость
- Качественная однородность единиц
Существует две категории средней величины:
- Степенные средние
- Структурные средние

Степенная средняя величина имеет две формы:
- Простая
- Взвешенная

Общая формула степенной средней простой:

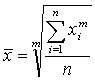
в зависимости от m различают виды:
1. m=1 – среднее арифметическое

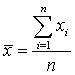
2. m=2 – квадратическая

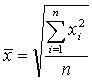
3. m=-1 – гармоническая

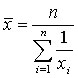
4. m=0 – геометрическая

5. кубическая

Взвешенная средняя величина
В качестве весов выступают числа единиц совокупности в разных группах.
Общая формула:

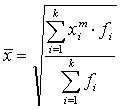
,где

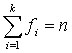
k- количество групп
f –частота
Для интервального ряда распределения x – середина соответствующего интервала.
Средняя арифметическая простая используется для расчета зарплаты.
Разновидность средней арифметической простой – средняя хронологическая:

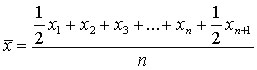
Средняя арифметическая взвешенная:

Область применения:
-Средняя квадратичная – показатель вариации
-Гармоническая – индекс теории
-Геометрическая – расчет среднего темпа роста

Правило мажерантности (старшинства средних величин)
Чем больше показатель m, тем больше величина:

Пример:
Оценки: 2, 3.

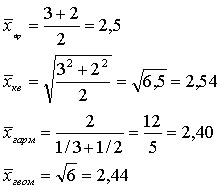, где 2,54>2,5>2,44>2,40
Структурные сведения характеризуют величину варианта, занимающую определенное положение в ранжированном вариационном ряду.
Мо – мода – наиболее часто встречающееся значение ряда.
Ме – медиана – соответствует варианту, стоящему в середине ряда.

Для дискретного ряда распределения Мо и Ме находятся с помощью таблицы:
Мо – максимальная частота
Ме – значение признака, при котором накопленная частота превышает половину численной совокупности.
Пример:
Х – разряд сотрудников, f – количество сотрудников.

x	f
2	2	2<10
3	6	8<10
4	3	11>10
5	5	&
6	4	&
ИТОГО:	20	&

Мо = 3 (наиболее часто встречающийся разряд = 6 человек).
Ме = 4 (11>10).
Вывод: 50% имеют разряд ниже 4, другие – выше.

Для интервального ряда распределения прежде чем определять точечные значения Мо и Ме находят модальный и интервальный Мо и Ме по тем же правилам, что Мо и Ме для дискретного ряда.
Точечные значения Мо и Ме определяются по формуле:

Квартили – делят совокупность на 4 части.

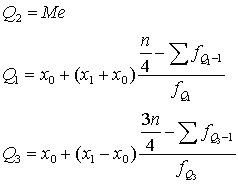
Пример 2:

x	f
85-95	3	3<10
95-105	10	13>10
105-115	1	&
115-125	2	&
125-135	3	&
135-145	1	&
ИТОГО:	20	&

Мо =?
Мода находится в интервале 95-105, Ме (медиана) находится в интервале 95-105 (n/2=10, 13>10) значит:

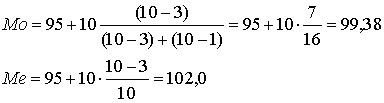
Вывод: половина предприятий выполнила норму менее 102%

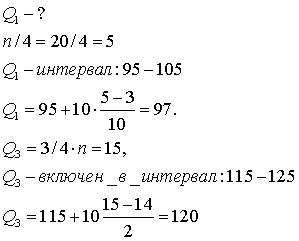
Вывод: ¼ предприятий выполняет норму менее 97%, ¾ - более 97% (Q3); ¾ предприятий выполняют норму меньше 120%, ¼ - больше 120%.
В симметричных рядах все показатели равны:

Графическое определение моды и медианы

Интервальный ряд изображают столбчатой диаграммой, основание которой – интервалы, высоты – частоты.
Вид диаграммы – гистограмма.
При увеличении числа наблюдений за одной и той же совокупностью, увеличивается число групп, что соответственно приводит к уменьшению величины интервала.
В этом случае ломанная, связывающая вершины столбиков превращается в плавную прямую – кривую распределения.
Если имеется дискретный ряд, то графическое изображение называется полигоном.
Для замыкания полигона крайние вершины соединяются на оси абсцисс отстоящей на 1 значение от максимального и минимального х.

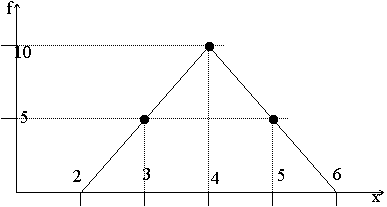
Мо и Ме можно найти графически .
Из графика видно, что Мо=Ме=4
(по данным примера 2)

Медиана определяется по кумулятивной кривой (кумуляте):

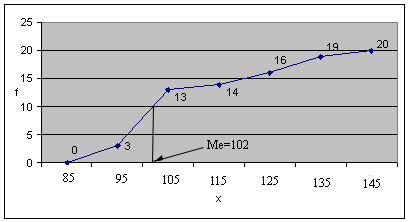
Показатели вариации. Определения.

Показатели:
1. размах вариации – из меньшего значения вычитается меньшее (R=Xmax-Xmin):

не обладает средней мерой колеблемости, используется для определения количества интервалов.
2. среднее линейное отклонение – средний модуль отклонений вариантов (х) от среднего арифметического значения х.
Для расчета используется формула средней арифметической простой (для не сгруппированных данных):

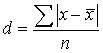
и взвешенной простой для сгруппированных данных:

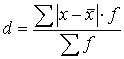
3. среднее квадратическое отклонение
Средняя квадратическая простая для не сгруппированных данных:

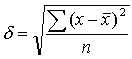
и взвешенная для сгруппированных данных:

4. дисперсия – средний квадрат отклонения – промежуточный показатель, используется для вычисления средней квадратической простой.
Является самостоятельным показателем, характеризующим меру вариации в очень однородных совокупностях с незначительной колеблемостью.
Простая:

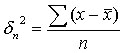
Взвешенная:

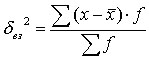
5. коэффициент вариации

используется для оценки интенсивности вариации. Совокупность считается однородной, если V не превышает 0,33.
Задача.
Рассчитать показатель вариации для интервального ряда по проценту выполнения норм.


85-95	90	3	270	17,5	52,5	306,25	918,75
95-105	100	10	1000	7,5	75,0	56,25	562,50
105-115	110	1	110	2,5	2,5	6,25	6,25
115-125	120	2	240	12,5	25,0	156,25	312,50
125-135	130	3	390	22,5	67,5	506,25	1518,75
135-145	140	1	140	32,5	32,5	1056,25	1056,25
ИТОГО:	-	20	2150	-	255,0	-	4375,00

X, f – дано. Остальные значения найдены по формулам в шапке таблицы.
Найдем:

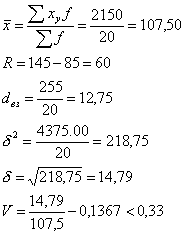
т.е. статистическая совокупность однородна.

Виды дисперсии. Правила сложения дисперсий.

После оценки средней величины признака, а так же его средней вариации, перед аналитиками встает вопрос об измерении силы влияния на этот признак других факторов.
На этом этапе исследования используют правило слежения дисперсий:
Общая дисперсия признака равна сумме межгрупповой дисперсии и средней из внутригрупповых дисперсий.

Межгрупповая дисперсия характеризует вариацию результативного признака под влиянием признака фактора, положенного в основу фактора.

Внутригрупповая дисперсия характеризует случайную вариацию результативного признака под влиянием неучтенных второстепенных факторов:

Средняя из внутригрупповых дисперсий:

На базе этих показателей оценки связи между признаками на базе эмпирического материала строят следующие показатели:
1. эмпирический коэффициент детерминации. Определяется как доля межгрупповой дисперсии в общей.
Характеризует силу влияния группировочного признака на результативный:

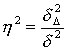
2. эмпирическое корреляционное отношение – корень квадратный из эмпирического коэффициента детерминации.
Характеризует тесноту связи.

Оба этих показателя находятся в пределах от 0 до 1.
0-связь отсутствует.
1-функциональная связь.
Для оценки тесноты связи с помощью корреляционного отношения используется шкала Чэддока:
0,1-0,3 – связь слабая
0,3-0,5 – умеренная
05,-0,7 – заметная
0,7-0,9 – тесная
0,9-0,99 – весьма тесная

Если изучаемое распределение близко к нормальному, то найденные показатели наиболее точно отражают характер изучаемого явления.

Развлечения:

Libo.ru

Полезное:

Информационная система Росии

Схема г.Москвы

MOLNET

Аудит и консалтинг

EURO-NEWS.RU

Контакты:

e-mail

ICQ:178194002

гостевая книга

форум